Machine Learning and Mathematics

The twin catalysts poised to accelerate twenty-first century mathematics: formalisation and machine learning.

In 1994, an anonymous group of mathematicians published a pamphlet titled The QED Manifesto¹. It set an ambitious goal — “to build a computer system that effectively represents all important mathematical knowledge and techniques” — essentially, to formalise all known mathematics and enable “the use of mechanical methods to check proofs”.

The manifesto stated nine core motivations for this grand endeavour, from accelerating research and improving confidence in published results, to improving software robustness, and even philosophical aspirations.

The QED system will provide a beautiful and compelling monument to the fundamental reality of truth. It will thus provide some antidote to the degenerative effects of cultural relativism and nihilism.

The QED Manifesto

While the manifesto acknowledged that its goal was “perhaps 300 years old”, it lamented the fragmentation of existing efforts and issued a rallying cry for coordination. A few conferences were organised around the QED manifesto in the years immediately following its publication, but beyond that the initial excitement around it appeared to fizzle out relatively quickly.

Follow-up research papers in 2007² and 2014³ examined the success of the manifesto. While acknowledging some “positive side-effects” and “substantial progress” in formalising theorems, they were mostly pessimistic, blaming the lack of progress on the fact that “only very few people are working on formalization of mathematics”, as well as noting that efforts so far had not done enough to serve mathematicians, with formalised mathematics bearing little resemblance to “real” mathematics.

Now, thirty years after the QED Manifesto was published, there are signs of progress. Formal mathematics is, if not thriving, certainly starting to gain more widespread adoption. Over the past decade, the increased interest in formal mathematics from the world of machine learning has accompanied new large-scale efforts at formalisation, novel tools for assisting formalisation, and the use of formalisation at the frontiers of mathematics.

One area where this has led to recent breakthroughs is in the world of competitive mathematics.

The International Mathematical Olympiad

First held in Romania in 1959, the International Mathematical Olympiad (IMO) is a prestigious annual mathematics competition for pre-university students. The 2024 IMO, held in the UK, featured contestants from over 100 countries⁴, with each country able to send up to 6 of its most promising young mathematicians as decided by selection processes sometimes involving multiple rounds of national competition.

Each IMO competition consists of six problems and is spread out over two days⁵. The problems are designed to be difficult, and generally require a high level of knowledge and ingenuity.

There are 7 points available per problem, and in the 2024 competition only one contestant got a perfect score of 42. The cutoff for a gold medal — in recent years, attained by fewer than 10% of participants — was 29 points. ⁶

Problem 1. Determine all real numbers α such that, for every positive integer n, the integer

$\lfloor \alpha \rfloor + \lfloor 2\alpha \rfloor + · · · + \lfloor n\alpha \rfloor$

is a multiple of n. (Note that $\lfloor z\rfloor$ denotes the greatest integer less than or equal to $z$ . For example, $\lfloor -\pi \rfloor = −4$ and $\lfloor 2 \rfloor = \lfloor 2.9 \rfloor = 2$ .)

Problem 2. Determine all pairs $(a, b)$ of positive integers for which there exist positive integers $g$ and $N$ such that

$\text{gcd}(a^n + b, b^n + a) = g$

holds for all integers n ⩾ N. (Note that $\text{gcd}(x, y)$ denotes the greatest common divisor of integers $x$ and $y$ .)

Problem 3. Let $a_1$ , $a_2$ , $a_3$ , … be an infinite sequence of positive integers, and let $N$ be a positive integer. Suppose that, for each $n > N$ , $a_n$ is equal to the number of times $a_{n-1}$ appears in the list $a_1$ , $a_2$ , … , $a_{n-1}$ .

Prove that at least one of the sequences $a_1$ , $a_3$ , a₅, … and $a_2$ , $a_4$ , $a_6$ , … is eventually periodic.

(An infinite sequence $b_1$ , $b_2$ , $b_3$ , … is eventually periodic if there exist positive integers $p$ and $M$ such that $b_{m+p} = b_m$ for all $m \geq M$ .)

Problem 4. Let $ABC$ be a triangle with $AB < AC < BC$ . Let the incentre and incircle of triangle $ABC$ be $I$ and $\omega$ , respectively. Let $X$ be the point on line $BC$ different from $C$ such that the line through $X$ parallel to $AC$ is tangent to $\omega$ . Similarly, let $Y$ be the point on line $BC$ different from $B$ such that the line through $Y$ parallel to $AB$ is tangent to $\omega$ . Let $AI$ intersect the circumcircle of triangle $ABC$ again at $P \neq A$ . Let $K$ and $L$ be the midpoints of $AC$ and $AB$ , respectively.

Prove that $\angle KIL + \angle YPX = 180\degree$ .

Problem 5. Turbo the snail plays a game on a board with 2024 rows and 2023 columns. There are hidden monsters in 2022 of the cells. Initially, Turbo does not know where any of the monsters are, but he knows that there is exactly one monster in each row except the first row and the last row, and that each column contains at most one monster.

Turbo makes a series of attempts to go from the first row to the last row. On each attempt, he chooses to start on any cell in the first row, then repeatedly moves to an adjacent cell sharing a common side. (He is allowed to return to a previously visited cell.) If he reaches a cell with a monster, his attempt ends and he is transported back to the first row to start a new attempt. The monsters do not move, and Turbo remembers whether or not each cell he has visited contains a monster. If he reaches any cell in the last row, his attempt ends and the game is over.

Determine the minimum value of n for which Turbo has a strategy that guarantees reaching the last row on the $n^{th}$ attempt or earlier, regardless of the locations of the monsters.

Problem 6. Let $\mathbb{Q}$ be the set of rational numbers. A function $f : \mathbb{Q} → \mathbb{Q}$ is called aquaesulian if the following property holds: for every $x, y ∈ \mathbb{Q}$ ,

$f(x + f(y)) = f(x) + y$ or $f(f(x) + y) = x + f(y)$ .

Show that there exists an integer $c$ such that for any aquaesulian function $f$ there are at most $c$ different rational numbers of the form $f(r) + f(−r)$ for some rational number $r$ , and find the smallest possible value of $c$ .

IMO Problems 2024, English.

Several successful IMO participants have gone on to become prominent mathematicians. IMO gold medalists who later won a Fields Medal⁷ include Maryam Mirzakhani, Peter Scholze, and Tim Gowers. Grigori Perelman, also an IMO gold medalist, was offered a Fields Medal and a $1m Millennium Prize for his solution of the Poincaré conjecture⁸.

Another now-prominent mathematician with a history of success in the IMO is Terence Tao. Tao first participated in the 1986 IMO at the age of 10, winning a bronze medal. The year after, he won a silver medal. In 1988, on his third and final time participating, aged 13, he won a gold medal. Since then, he has gone on to win a Fields Medal and has published hundreds of research papers spanning an unusually broad range of mathematical disciplines.

The IMO’s association with mathematical ability is what makes it such an alluring benchmark for automated mathematical reasoning systems, and it is therefore no surprise that leading AI research labs have set their sights on the IMO.

In September 2019, researchers from Microsoft, Google, Imperial College London, The University of Pittsburgh, and Stanford University suggested running an IMO Grand Challenge⁹ — a version of the IMO for AI systems.

In the following years, leading AI research labs including OpenAI¹⁰, Google DeepMind¹¹ and Meta¹² have published research showing their progress towards automated systems for solving IMO problems.

But there’s a crucial distinction here: the problem statements fed to these automated systems are not the same as those given to student participants of the IMO. The solutions take a different form, too.

These systems use what’s known as formal mathematics.

Formal Mathematics

Although mathematics is a precise and rigorous field, most mathematics is actually informal: it uses a mix of natural language (English, in the examples here) and mathematical terms. It relies on some level of subjective judgement by the author to decide which steps “follow” from others, and which statements can be considered “obvious”.

Consider the following problem and its proof.

$\text{Prove that there is no positive}$ $\text{integer } n$ $\text{for which }$ $2^n + 1$ $\text{is divisible by 7.}$

Statement of IMO 1964P1b, as given to student competitors.

$2^3 = 1 \text{ (mod 7)}$ .
$\text{Hence } 2^{3m} = 1 \text{ (mod 7)}, 2^{3m+1} = 2 \text{ (mod 7)}, \text{ and } 2^{3m+2} = 4 \text{ (mod 7)}$ .
$\text{Hence we never have 7 dividing } 2^n + 1$ .

Informal Proof of IMO 1964P1b, slightly modified. Source

At no point does the proof explicitly state that $\text{x is divisible by 7}$ is equivalent to $x = 0 \text{ (mod 7)}$ ; this is considered obvious. It is also not explicitly stated that any positive integer $n$ must take one of the three forms $n = 3m$ , $n = 3m + 1$ , or $n = 3m + 2$ , for some value of m¹³.

These are both elementary facts of number theory, and most mathematics students would indeed consider them obvious. Nonetheless, as proofs get longer, more complicated, more abstract, and span wider areas of mathematics, the line between “obvious” and “requires justification” gets blurrier.

When it comes to informal proof, mistakes arise from gaps in the reasoning, appeal[s] to faulty intuitions, imprecise definitions, misapplied background facts, and fiddly special cases or side conditions the author failed to check.

There is an alternative: formal mathematics. The history of formal methods in mathematics goes back at least a century¹⁴. In essence, a formal proof is one performed within the constraints of a formal system: a combination of a formal language, a set of inference rules, and a set of axioms. These are the building blocks of the new mathematical foundations that the QED Manifesto set out to build.

Generating a proof within a formal system consists of using the available inference rules to derive a new theorem from the starting axioms or previously proved theorems — all expressed in the formal language. These formal proofs have the significant benefit of allowing for verification, in that their correctness can be verified through a straightforward mechanical procedure — one that can be performed by a computer algorithm.

The drawback is that formal languages, due to their need for precision, can seem extremely verbose and can be cumbersome to deal with directly. The example below from Russell and Whitehead’s Principia Mathematica, published at the beginning of the 20th century, demonstrates this verbosity.

Several lines of proof containing unfamiliar symbols, ending with the line "From this proposition it will follow, when arithmetical addition has been defined, that 1 + 1 = 2." — Excerpt from page 379, volume 1 of Principia Mathematica (1910).

Early computer approaches to formal proofs focused on solving this problem through full automation, and it wasn’t until the late 1960s that a new approach came about. This approach focused on allowing users to interact with a computer program called a proof assistant (also sometimes called an interactive theorem prover); a tool for writing formal proofs¹⁵.

As an interface between the thinking mathematician and the precise formal proof artifact, one of the proof assistant’s jobs is to enable the mathematician to perform higher-level operations which are then translated into the verbose formal language.

For example, proving the identity $(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$ might be laborious in the formal proof language, but with some automation these types of straightforward algebraic equalities can be resolved by the user invoking a single command, which generates the required low-level proof steps in the background¹⁶.

These higher-level user commands are called tactics. Modern proof assistants such as Lean¹⁷ — a free and open-source proof assistant first developed by Leonardo de Moura at Microsoft Research in 2013 — have tactics that provide a powerful layer of abstraction, enabling them to do things like breaking statements up into cases, applying known results, simplifying expressions, and performing induction — making formal proof construction more accessible, and more familiar, to mathematicians.

The proof below is a formal version — using the Lean proof assistant — of the earlier informal IMO proof.

import Mathlib.Tactic
open Nat

theorem imo_1964_p1b (n : ℕ) : ¬ 7 ∣ (2^n + 1) := by
  intro h
  apply mod_eq_zero_of_dvd at h
  have h1: 2 ^ 3 % 7 = 1 := by rfl
  mod_cases h2 : n % 3 <;> rw [←div_add_mod n 3, h2] at h
  · rw [zero_mod, add_zero, add_mod, pow_mod, pow_mul, pow_mod, h1, one_pow] at h
    contradiction
  · rw [add_mod, pow_add, pow_mul, mul_mod, pow_mod, h1, one_pow] at h
    contradiction
  · rw [add_mod, pow_add, pow_mul, mul_mod, pow_mod, h1, one_pow] at h
    contradiction

Lean proof of IMO 1964 problem 1, part b. Source: compfiles

The Lean proof invokes the Nat.mod_eq_zero_of_dvd lemma¹⁸ in the first step, using the apply tactic. This particular lemma proves that if a number is divisible by n, it must be equal to zero mod n. In the informal proof shown earlier, this step was omitted.

The rest of the Lean proof follows a similar line of argument to the informal proof. It introduces a new hypothesis, h1, and uses the rfl (“reflexivity of equality”) tactic to prove it. It then uses the mod_cases tactic to split the remaining proof into three cases, for the three values that n can take modulo 3 (again, something used but not explicitly stated in the informal proof).

Each of these three cases is dealt with using the rw (“rewrite”) tactic, sequentially invoking lemmas to do straightforward rewrites of the remaining algebraic expressions.

For example, the zero_mod lemma establishes that $\text{0 mod m = 0}$ , and the one_pow lemma shows that $1^m = 1$ , for any natural number $m$ . In practice, in longer Lean proofs, higher-level tactics like simp (“simplify”) might be used to do this instead.

Once we can show in each case that the expression evaluates to a value other than zero, the contradiction tactic closes the goal — effectively showing that assuming $7 | (2^n + 1)$ always leads to a contradiction, and so this assumption must be false.

An interactive version of this proof, which allows inspection of the state at each proof step, is available in the Lean 4 web editor.

It’s worth noting that the Lean proof above is not, itself, a formal proof that is directly verifiable by the Lean kernel. It would be more accurate to interpret it as a series of commands that Lean uses to produce a low-level proof that can be computer-verified. The low-level proof is much longer, more verbose, and harder (for humans) to interpret.

This distinction between the low-level (directly verifiable) layer and the higher-level layers makes modern proof assistants like Lean particularly powerful. Lean’s high-level tactic framework is highly extensible — users can write their own tactics, and a library of shared tactics is available within mathlib — a public repository of Lean tactics, definitions, and proofs. One way this has been described is that “tactics create candidates for proofs, and then the kernel checks that they are actually correct proofs”¹⁹.

This process of flexible candidate generation and robust verification leads very naturally into the world of machine learning and large language models (LLMs). While LLMs can be error-prone and unreliable, they are good at ingesting large bodies of text (during training) and then generating next-phrase suggestions based on a particular context (at inference time). This, then, seems like a natural fit: train an LLM on the existing corpora of formal proofs, and then have it attempt to generate a valid proof step-by-step. At each step, the proof assistant kernel can check that the proof step is valid, and it can also confirm when the proof is complete.

[LLMs] are fundamentally unreliable, but it turns out this lack of reliability does not matter if we use the language model to generate formal proofs of theorems we have already stated, since the proof assistant’s kernel can check the proof in the end.

This approach is the basis of much of the machine-learning-based theorem proving work from recent years.

Automating Formal Proofs

The 2010s saw the rapid development and adoption of deep learning — training multi-layer neural networks on large data sets through the process of backpropagation of errors and stochastic gradient descent. Successes in image recognition were followed by the birth of deep reinforcement learning (deep RL) — combining deep learning techniques with reinforcement learning, where agents are trained to behave optimally in environments over multiple steps.

Deep RL had a string of successes in Atari games , two-player board games , and other environments, and was later instrumental in transforming pre-trained language models like GPT-3 into useful dialogue-capable models like ChatGPT through reinforcement learning with human feedback .

The two developments in this period that have turned out to be most relevant to automated theorem proving are generative text models (like GPT) and model-based deep RL approaches (like AlphaZero).

Generative text models²⁰ can usefully represent the semantics of text-like sequences (whether natural language, programming languages, or formal proofs), and generate additional sequences based on an input sequence. These sequence pairs can be framed as dialogue responses, translation between languages, or “guessing” the next step in a proof. LLMs fall into this category of models.

Model-based deep RL approaches can, given a model or simulator of a game, work out a winning approach (often referred to as a policy) by repeatedly playing a simulated version of the game, intelligently exploring the tree of potential moves, and iteratively building a representation of the relative value of each potential move from a given position.

DeepMind famously used model-based deep RL in their AlphaGo agent, which in 2016 beat world champion Lee Sedol in a five-game match of Go²¹. While this particular agent had initially learned to play from a large dataset of human Go games, DeepMind’s follow-up agent — AlphaZero — surpassed AlphaGo’s performance while teaching itself entirely from scratch through self-play.

It is this AlphaZero agent that is often referred to in recent deep RL approaches to automated theorem proving. In the version of AlphaZero that played grid-based board games, a convolutional neural network was trained through self-play to produce a probability distribution over next moves, as well as the win probability of game states.

A direct example of how this can be adapted for proof search is found in Meta’s 2022 HyperTree Proof Search (HTPS; ) paper, which the authors say is “inspired by” AlphaZero, and builds upon the earlier GPT-f paper by OpenAI along similar lines . In the HTPS approach, encoder-decoder transformer models are trained to output a probability distribution over the next proof token²², and to estimate the probability that a goal is provable from a given proof state. This shows a relatively direct mapping between the value of moves in a game and the value of steps in a proof. The issue of the unboundedness of the action space — the fact that, unlike in chess or Go, a step in a proof isn’t chosen from a finite list of candidates (given that proof steps can be arbitrarily long strings) is dealt with by sampling actions from a language model, token by token.

Because these proofs are written in a formal language, the corresponding proof assistant program can confirm whether a potential “move” — i.e. a proposed proof step — is valid; a critical efficiency in an exponentially growing search (hyper)tree. The proof assistant can also attest that the resulting artifact is a correct and complete proof; however terse or meandering the proof might be.

Like games, formal mathematics has an automated way of determining whether a trajectory (i.e. a proof) is successful (i.e. formally correct). But the vast scope of formal mathematics means that any strong reasoning result obtained in it will be more meaningful than comparable results in games (e.g. finding proofs to mathematical conjectures), and could even be applicable to important practical problems (e.g. software verification).

As of late 2024, the state of the art on IMO problems is represented by two Google DeepMind systems which incorporate some of these ideas: AlphaProof, and AlphaGeometry 2.

AlphaProof

On a Thursday in late July 2024, a few days after the conclusion of the IMO and on the eve of the “AI for math” workshop at the International Conference for Machine Learning, Google DeepMind published a blog post announcing “AI achieves silver-medal standard solving International Mathematical Olympiad problems”.²³

The newly-announced approach combined two systems: AlphaProof, a new deep-reinforcement-learning-based system for formal mathematical reasoning, and AlphaGeometry 2, an improved version of a geometry-solving system first published six months earlier.

Given formal versions of the six questions in the 2024 IMO, it solved four completely: one geometry problem solved by AlphaGeometry, and three problems solved by AlphaProof (two in algebra and one in number theory). This would give it 28 points out of a maximum of 42, just one point short of the 29 required to get a gold medal in the 2024 IMO.

AlphaProof is a system that trains itself to prove mathematical statements in the formal language Lean. It couples a pre-trained language model with the AlphaZero reinforcement learning algorithm, which previously taught itself how to master the games of chess, shogi and Go.

AlphaProof blog post, Google DeepMind, July 2024

There is no detailed technical paper to accompany the AlphaProof blog post yet, but based on the available details, the system embraces the model-based deep RL approach with its use of AlphaZero, and relies on an enormous amount of synthetic data: around a million mathematics problems were automatically translated into formal Lean statements using a version of Google’s Gemini model which was fine-tuned for auto-formalisation. For the final evaluation, AlphaProof was given formalised versions of the IMO problems in Lean to solve.

"AlphaProof system diagram, showing around 1m informal problems being fed into a formaliser network, generating around 100 million formal problems. These are then passed to the search-train loop between the solver network and formal proofs, which constitute the ALphaZero part of the system." — Source: Google DeepMind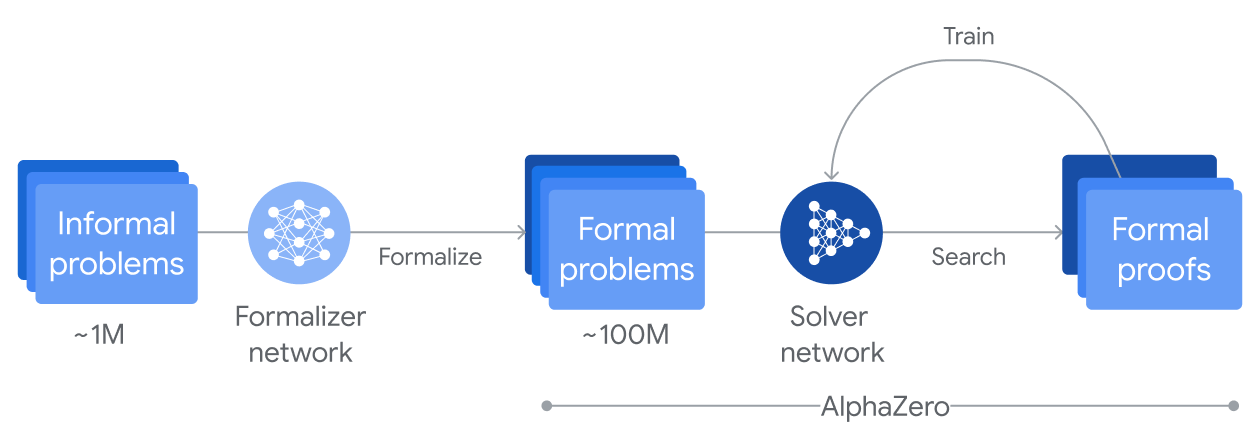

In addition to the initial training set, AlphaProof also stores the intermediate proof results that it generates, and uses them to retrain its solver network as it learns to solve progressively more difficult problems — mirroring the goal of the QED manifesto, and bootstrapping itself into a system with a broad representation of mathematical knowledge.

It seems likely that significant computational resources are required for AlphaProof at both train and test time. The release blog post states that the system took “up to three days” to solve some of the problems, in contrast to the average time of 90 minutes per problem that human participants get. This clock time estimate does not directly tell us anything about the resources used, however. The 2017 version of AlphaZero, playing board games in a finite action space, used “a single machine with 4 TPUs”²⁴. Given Google DeepMind’s ability to access vast computational resources and the benefit to be gained from parallelisation across these resources, it is possible that significantly more test-time compute was used for AlphaProof.

AlphaGeometry

The second component of Google DeepMind’s IMO silver-medal-level system is AlphaGeometry 2. This is a more powerful version of their earlier AlphaGeometry system, with a new language model trained on more data, a faster symbolic engine, and a new “knowledge-sharing mechanism”. AlphaGeometry 2 solved the IMO 2024 geometry problem within 19 seconds.

Not much technical detail is available on AlphaGeometry 2, but the original AlphaGeometry — announced in January 2024 — was accompanied by a Nature paper describing the system, a public repository with the source code, and downloadable model weights. At the time of its initial publication, AlphaGeometry’s performance was close to the level of an IMO gold medallist on Euclidean plane geometry problems²⁵. Unlike AlphaProof, which uses Lean, AlphaGeometry uses a different geometry-specific formal mathematics language.

AlphaGeometry is a neuro-symbolic system made up of a neural language model and a symbolic deduction engine, which work together to find proofs for complex geometry theorems. Akin to the idea of “thinking, fast and slow”, one system provides fast, “intuitive” ideas, and the other, more deliberate, rational decision-making.

Google DeepMind blog post

AlphaGeometry’s approach is different to AlphaProof’s, too. Rather than using AlphaZero, it builds on top of a powerful symbolic system which is able to deduce new facts from a set of known facts, enhancing it with the addition of a language model that is trained on synthetic data to generate new constructions.

The AlphaGeometry system has several key components:

A deductive database (DD), able to mechanically deduce new statements from given premises.
An algebraic reasoning (AR) engine, able to solve systems of linear equations to perform angle-, ratio-, and distance-chasing.
A language model that can suggest new constructions.

The symbolic component of the system, iterative alternated application of depth-first search using the deductive database and the algebraic reasoning engine, is already very powerful in itself, and able to solve 14 of the 30 problems in the benchmark dataset, while the full AlphaGeometry system is able to solve 25 of them²⁶.

DD and AR are applied alternately to expand their joint deduction closure. The output of DD, which consists of new statements deduced with deductive rules, is fed into AR and vice versa… This loop repeats until the joint deduction closure stops expanding.

The full AlphaGeometry, when presented with a problem, first attempts to solve it using the purely symbolic system comprised of DD and AR. If that fails, it performs beam search over the top 512 auxiliary constructions suggested by the language model, each time running the symbolic system to check whether the auxiliary constructions are sufficient to reach the proof goal.

As a simplified concrete example to demonstrate how the neural and symbolic parts of the system interact, consider the problem in the example below, taken from the AlphaGeometry paper. The problem asks us to prove that if a triangle ABC has two sides of the same length — $AB=AC$ — then angle $\angle ABC$ is the same as angle $\angle BCA$ .

Three-stage graphic showing, first a triangle ABC with the statement "Let ABC be any triangle with AB=AC. Prove that angle ABC = angle BCA. In the second step, it shows AlphaGeometry going between the symbolic deduction engine and the language model, until the problem is solved. Step three shows the solution, using the construction of an additional point D as described below. — Source: AlphaGeometry repository on GitHub, cropped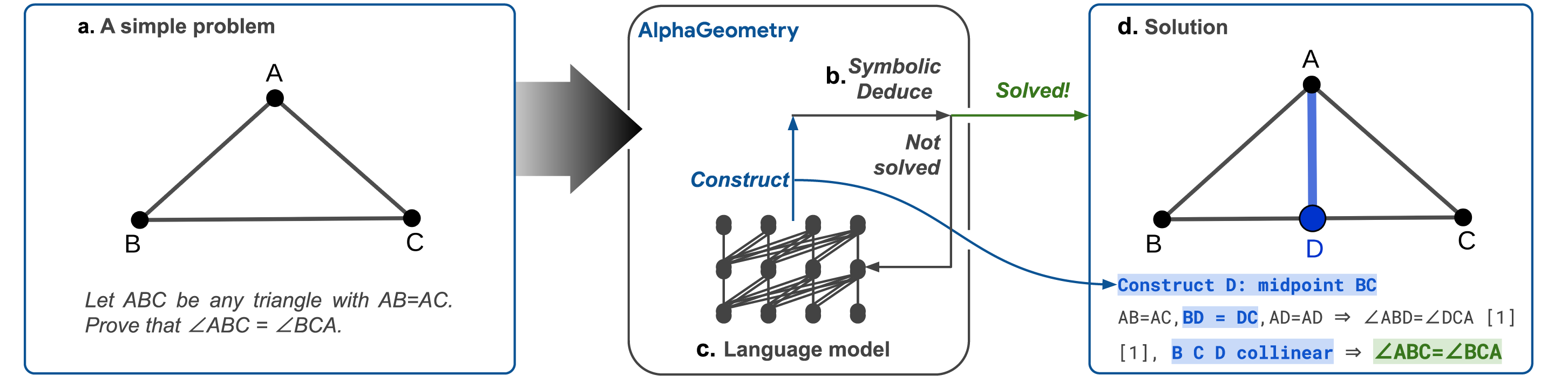

An easy way to prove this is to “construct” an additional point D, at the midpoint of the line BC. This construction does not change the nature of the problem; it just labels the midpoint of BC so that the system can reason about it explicitly. With this extra point in place, it follows that the angles $\angle ABD$ and $\angle DCA$ are the same, since they’re part of triangles with identical length sides. Since D lies on the same line as B and C, it then follows that $\angle ABC = \angle ABD = \angle DCA = \angle BCA$ .

In this example, the construction of the additional point D unlocked the rest of the proof. In AlphaGeometry, it would be the language model’s job to suggest D as a construction, at which point the deductive database would be able to perform the rest of the proof. In this simple example, the algebraic reasoning component would not be needed.

This particular problem required only one straightforward auxiliary construction. The power of the language model comes from its flexibility, as the complexity of the problems and number of required constructions increases. IMO-level geometry problems can require several constructions, and the space of possible constructions can be large. Sampling suggested constructions from the LLM allows for a broader — but still targeted — search of relevant constructions compared to merely using a pre-defined list of construction heuristics.

What’s next?

Google DeepMind’s 2024 IMO solutions, awarded full marks on 4 out of the 6 problems, came only one point short of a gold medal score. There is no sign yet of progress slowing down, and — somewhat dependent on the make-up of problems²⁷ — it seems likely that an AI system will reach the gold medal standard at the next IMO in July 2025.

The IMO is only the beginning. Once there are models that can reliably achieve gold medal standard in the IMO, or a perfect score, there will be harder benchmarks for them to tackle. As one example, the William Lowell Putnam Mathematical Competition is an annual mathematics competition for undergraduate students in the US and Canada. Researchers at UT Austin have created a dataset — PutnamBench — with formalised versions of over 600 previous problem statements from this competition, in Lean as well as other formal proof languages.

So far, the best system evaluated on this benchmark was only able to solve around 1% of past problems²⁸, however this benchmark has not yet received anywhere near the level of effort or attention that the IMO has. Requiring undergraduate-level mathematics knowledge and techniques makes this benchmark harder than the IMO, though it is currently not clear just how much harder. There are hurdles even at the most basic level, as Lean’s mathlib library does not yet cover all undergraduate mathematics²⁹.

Alongside the established industry labs working on automated theorem proving, new startups, like Harmonic, which raised a $75m Series A in September 2024³⁰, are also entering the field.

And there’s a burgeoning open community too. In November 2023, XTX Markets announced a $10m commitment to a prize fund for an Artificial Intelligence Mathematical Olympiad (AIMO) prize; in some sense a concrete instantiation of the IMO Grand Challenge. The first progress prize task, hosted on Google’s Kaggle platform, ended in July 2024, and the top prize of around $130k was won by team Numina, with support from Hugging Face, MistralAI, Answer.ai, General Catalyst, and Beijing CMLR.

The second progress prize, with at least $260k up for grabs for the top team, closes in April 2025. Both these progress prizes use natural-language problem statements of IMO-like problems with integer solutions between 0 and 999. This is intended as a stepping stone towards a challenge with natural language IMO problems and natural language answers, in line with the standard IMO setup.

This touches on a point worth reiterating: much of the impressive progress has been in the domain of formal mathematics, where algorithms can explore the solution space in a guided way, with rich feedback. Though a model which could reliably ingest formal versions of IMO problem statements and output formal solutions is clearly a step towards an “AI IMO gold medalist” from the current status quo, it is unclear how much of the distance it covers.

Auto-formalisation — turning natural language problem statements into formal problem statements in an automated way — is not a solved problem, and neither is its converse, auto-informalisation. There is not always a unique or even a clear canonical formalised version of an informal statement, and seemingly small distinctions in the formal statement definition can have a large impact on how challenging the statement is to prove.³¹ Despite the difficulty, progress is clearly being made in auto-formalisation, as demonstrated by the AlphaProof team’s auto-formalisation of large numbers of informal problems as training data.

There is also ongoing research on natural language mathematical problem-solving. Benchmarks like GSM8K and MATH contain natural language problems and solutions from elementary to high school competition level, and published benchmark scores for LLMs on these datasets have been improving over time. However, there is some concern that language models are overfitting to these particular benchmarks, and the static nature of these benchmark data sets comes with a risk of test set leakage. Some recent papers have called into question the validity of improving benchmark scores, and have shown the brittleness of some natural language approaches³².

The FrontierMath benchmark , announced by Epoch AI in November 2024, aims to address some of these issues. It contains hundreds of original and difficult mathematics problems contributed by leading mathematicians, which “typically require hours or days for expert mathematicians to solve”.

Despite the concerns about benchmark overfitting, it does appear that progress is being made on natural language mathematical reasoning. OpenAI’s o1 series of models³³ use additional inference-time compute to “reason through complex tasks”, improving the models’ performance on natural language mathematics and related benchmarks.

Google DeepMind, too, in their AlphaProof blog post, noted that they tested a natural language reasoning system, based on their Gemini language model, on IMO problems, and that the system showed “great promise”.

It would be reasonable to ask: to what end? Are these advances useful beyond competition mathematics? Can they contribute to “real” mathematics — for example, are they relevant at the frontiers of mathematics research?

The Impact on Mathematics Research

The successes discussed so far all relate to the arguably-somewhat-artificial world of competition mathematics, where problems with known solutions are posed to mathematics students.

Research is different: mathematicians work to advance the frontiers of knowledge, studying questions to which the research community doesn’t yet know the answer (or whether there even is one). Sometimes the hardest part is working out which question to ask, or which questions are most likely to yield solutions when pressed. Research problems are much more difficult than competition problems, and the accompanying longer proofs lead to exponentially harder proof search.

Computers have been used to prove novel results since at least the 1970s, though at first arguably more in the sense of proof automation than proof discovery, particularly for problems which require considering large numbers of cases.

For example, mathematicians in the 1850s conjectured that in order to colour any map (for example, a map of countries or states) in a way that no neighbouring regions share a colour can always be done by using at most four different colours. There is a long history of incorrect-though-temporarily-accepted proofs of this result. Most recently, in the 1976 proof by Kenneth Appel and Wolfgang Haken, which made extensive use of computer programming to evaluate over one thousand cases representing different configurations of regions, flaws were found a few years after publication. The flaws were resolved, and a corrected (and now widely accepted) proof was published in 1989 .

This result — known as the four colour theorem — is one of the first major computer-assisted proofs. These proofs came with additional burdens on reviewers, who would have to either painstakingly review the case-by-case analysis produced by the computer programs, or review the computer programs themselves in minute detail.

Formal proofs provide an alternative method of verification. In 2005, a formal proof of the four-colour theorem was developed using the Coq proof assistant , enabling anyone who trusts the Coq kernel to trust that the proof is correct. Similarly, other proofs, including those of the odd order theorem and the Kepler conjecture have been formalised and verified. Formalising the proof of the Kepler conjecture took over 10 years .

How is trusting a proof assistant any better than trusting other pieces of software?

In discussions of formally verified mathematics, the following question often arises: Proof assistants are complex pieces of software, and software invariably has bugs, so why should we trust such a program when it certifies a proof to be correct?

Proof assistants are typically designed with an eye toward minimizing such concerns, relying on a small, trusted core to construct and verify a proof. This design approach focuses concern on the trusted core [the “kernel”], which consists of, for example, approximately 400 lines in Harrison’s HOL light system. Users can obtain a higher level of confidence by asking the system to output a description of the axiomatic proof that can be checked by independent verifiers; even if each particular verifier is buggy, the odds that a faulty inference in a formal proof can make it past multiple verifiers shrinks dramatically. It is even possible to use formal methods to verify the trusted core itself.

It’s not only long computer-assisted proofs that benefit from formalisation. Recently Terence Tao has been formalising some of his work in Lean, and sometimes finding errors in the process.

As a consequence of my #Lean4 formalization project I have found a small (but non-trivial) bug in my paper!

Enclosed is the specific point where the formalization failed; Lean asked me to establish $0 < n - 3$ , but the hypothesis I had was only that $n > 2$ , and so the “linarith” tactic could not obtain a contradiction from the negation of $0 < n - 3$ .

Terence Tao, Mathstodon, October 2023

The proof of the polynomial Freiman-Ruzsa (PFR) conjecture, after decades of attempts and a recent collaboration between Terence Tao, Tim Gowers, Ben Green, and Freddie Manners, was published on arXiv in November 2023 . Tao led a team of volunteers in a formalisation effort, and the formalisation was finished within a few weeks³⁴.

Formalising proofs is hard work, and quite different to writing “informal” (standard) mathematical proofs. Regarding the PFR formalisation, Tao noted that he “…found that the most mathematically interesting portions of the project were relatively straightforward to formalize, but it was the technical ‘obvious’ steps that took the longest”.³⁵

In his 2022 paper titled “How can it be feasible to find proofs?”, Tim Gowers mentioned that while generating formal proofs is currently still hard work, once higher-level and more mathematician-friendly tools are developed to help mathematicians produce formal proofs, formal proofs could become the norm — “it is likely that there will be a cultural shift, and that what mathematicians understand by ‘proof’ will be more like ‘formally verified proof’” .

Beyond verification, formalisation also has significant benefits for collaboration. Collaborating on formal mathematics can look a lot like editing a codebase with extensive unit tests — it’s possible to edit small parts of a system without worrying about breaking things. This also makes it possible to delegate parts of a proof to previously unknown collaborators. As per, once again, the prolific Terence Tao, on the process of formalising PFR: “…it makes large-scale mathematical collaboration possible without necessarily having a pre-established level of trust amongst the collaborators; my fellow repository maintainers and I have already approved several pull requests from contributors that had not previously met, as the code was verified to be correct and we could see that it advanced the project.”³⁶

But not only that: formal proofs have structure, and this structure can be used to oversee collaboration. It’s common when writing formal proofs to first write down all the intermediate results that need to be proved, leaving gaps in the proofs to be filled in later (Lean uses the keyword sorry to indicate missing parts of proofs).

The Lean Blueprint tool allows researchers to map each of these intermediate results to a human-readable form, and display a dependency graph, colouring theorems and lemmas by their state (whether a node’s dependencies/statement/proof/ancestors are formalised), giving collaborators insight into the project state and giving interested observers an overview of the proof as a whole.

A large directed graph containing blue, green, and white nodes. The PFR theorem node is near the bottom, and the graph above shows the status of all the dependencies. — PFR blueprint. Source: Terence Tao's blog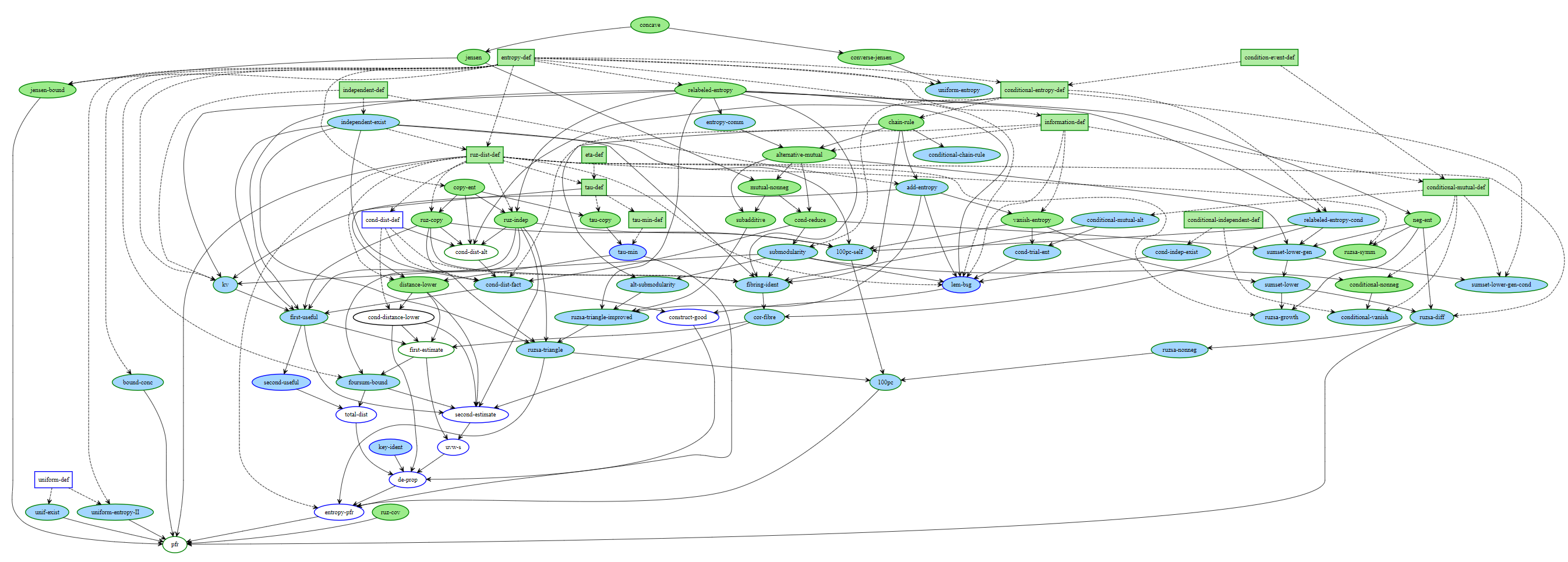

For an interactive example, see the live dependency graph for Emily Riehl’s ongoing ∞-Cosmos project.

For now, formalised results make up only a tiny fraction of all known mathematics results. Certain areas of mathematics are better represented than others in the libraries of formal proofs. Not only that, but formal proofs in one language don’t translate automatically to other languages.

Freek Wiedijk — author of the “QED Manifesto Revisited” paper — maintains a list of 100 notable theorems and their formalisation status in different proof assistants. As of November 2024, Isabelle is top of the list with 91 out of the 100 theorems formalised, HOL Light is second with 87/100, Coq is third with 79/100, and Lean is fourth with 76/100 theorems formalised. To some extent this reflects their ages — Lean has been around for just over a decade; Isabelle was first released in 1986.

Only one of the 100 theorems has yet to be formalised using any proof assistant: the infamous Fermat’s Last Theorem (FLT). The deceptively simple result, first conjectured by Pierre de Fermat in the 17th century, states that the equation $a^n + b^n = c^n$ does not have any non-zero integer solutions for $n>2$ (unlike the case $n=2$ , where, say, $3^2 + 4^2 = 5^2$ ). It took over three hundred years before a successful proof was developed, by Andrew Wiles, in 1994, with help from Richard Taylor. The proof is long — the paper presenting it is over 100 pages — and spans multiple areas of mathematics including group theory, algebraic geometry, and Galois theory.

Kevin Buzzard — who gave a special plenary lecture on formal mathematics at the 2022 International Congress of Mathematicians — has embarked on a multi-year project to formalise a modern proof of Fermat’s Last Theorem in Lean. The project started in October 2024, and has secured funding for the next five years.

/-- Statement of Fermat's Last Theorem
    over a given semiring with a specific exponent. -/
def FermatLastTheoremWith (α : Type*) [Semiring α] (n : ℕ) : Prop :=
  ∀ a b c : α, a ≠ 0 → b ≠ 0 → c ≠ 0 → a ^ n + b ^ n ≠ c ^ n

/-- Statement of Fermat's Last Theorem
    over the naturals for a given exponent. -/
def FermatLastTheoremFor (n : ℕ) : Prop := FermatLastTheoremWith ℕ n

/-- This is now a theorem of Wiles and Taylor--Wiles;
    see https://github.com/ImperialCollegeLondon/FLT
    for an ongoing Lean formalisation of a proof. -/
def FermatLastTheorem : Prop := ∀ n ≥ 3, FermatLastTheoremFor n

Lean statement of Fermat’s Last Theorem. Source: Mathlib

Lean’s mathlib library contains over 5,000 files with a total of more than 1.6m lines of code³⁷, but is still missing large amounts of relevant mathematics, including some undergraduate topics. Formalising more of mathematics — “to help computers understand what we are doing in modern mathematical research” is one of Buzzard’s motivations³⁸. He has noted that Lean is still lacking support for number theory, making it impossible “to even state” results being discussed in number theory seminars in Lean, “let alone to check their proofs”.

The process of proving FLT in Lean will require adding support for numerous mathematical concepts to Mathlib, including “automorphic forms and representations, Galois representations, potential automorphy, modularity lifting theorems, the arithmetic of varieties, class field theory, arithmetic duality theorems, Shimura varieties and many other concepts used in modern algebraic number theory”.

The research examples presented so far are post-hoc formalisations, where known proofs were formalised. There are also research projects where formalisation plays a key role during proof development. Terence Tao’s Equational Theories Project, started in September 2024, set out to establish relationships between all 4,694 single-equation laws of magmas³⁹ involving at most four magma operations. This amounts to proving or disproving over 22 million implications. The project was crowd-sourced, with infrastructure to track informal and formal (Lean) proofs of each of the equations. Some proofs were generated using automated theorem provers like Vampire, whereas others were manually developed by contributors. Formalisation allowed organisers to rely on the validity of third-party contributions. As of late November 2024, there are 47 separate contributors on the project’s GitHub repository⁴⁰, all implications have been proved informally, and only 138 of the over 22 million implications are lacking a formal Lean proof.

A Killer Application

Back in 2007, Freek Wiedijk gave two reasons why the QED manifesto’s aspiration to formalise all known mathematics had not yet been achieved.

For one, he noted that formalised mathematics in the systems available at the time did not “resemble real mathematics”, and that proof assistants did not do enough to serve mathematicians. To some degree languages like Lean, with powerful metaprogramming abilities enabling high-level tactics, are a step towards addressing this.

The other reason he stated was that formalisation has no ‘killer application’.

… if one writes a formalization of a mathematical result, then one has to work quite hard, and then at the end one has a tar.gz file with several computer program-like files in it. However, unlike a computer program, those files have no immediate further use.

One of the motivations for the FLT formalisation reveals a killer application: formal proofs are assets that can be used to train computer systems that can “help mathematicians with their research, doing things from checking messy lemmas automatically to suggesting results which may be helpful in a given situation”, per Kevin Buzzard⁴¹.

Indeed, machine-learning-based tools are already useful for assisting formalisation efforts. In November 2023, Terence Tao specifically mentioned chat, auto-complete, and semantic search tools as being helpful⁴².

Other tools like Lean Copilot and LLMLean aim to be special-purpose “copilots” for proof formalisation. Building on top of the Lean proof assistant, these tools can provide LLM-generated suggestions for proof steps. Unlike more generic code auto-complete tools like GitHub Copilot, suggestions in these tools are checked before being shown to the user, and so are guaranteed to be valid statements.

In a sense, then, formalised mathematics is also a ‘killer app’ for generative AI — one of few applications where hallucinations can be harnessed for good, feedback is cheap and reliable, and synthetic data is plentiful.

This symbiotic relationship is already yielding results in the form of progress on automated mathematics at IMO level and useful tools for developing formal proofs, and research labs seem set to continue to allocate resources to both formalisation and automated theorem proving. Meanwhile, adoption of proof assistants like Lean continues to grow among working mathematicians, and repositories of formal mathematics like Lean’s mathlib continue their advance across the field of known mathematics. If these trends continue, automated systems built on formal mathematics will continue to become more powerful and useful.

While the QED manifesto has not been successful yet, the dream behind it is more alive than ever.

For a hands-on introduction to formal proof in Lean, see The Natural Numbers Game. The free online Theorem Proving in Lean book gives a more in-depth overview. The Lean community website has links to other resources as well as events and the Zulip live chat.

For a broader look at the intersection between AI and mathematics, there’s an incredibly helpful public Google Doc initially put together as part of an “AI to Assist Mathematical Reasoning” workshop.

The letters QED, short for the latin quod erat demonstrandum, meaning “that which was to be demonstrated”, are used to proclaim the end of a mathematical proof. A version of the QED manifesto can be found here. It is now known that the mathematician Robert Boyer was one of the main people behind the manifesto. ↩
See . ↩
See , written by the chairs of a 2014 conference to celebrate 20 years of the QED project. ↩
More information on IMO contestants is available on the IMO website. ↩
On each day, participants get given three problems to attempt to answer over 4.5 hours. Participants are not allowed to use a calculator, smartphone, or reference resources like notebooks or tables. ↩
Source: IMO results by year. ↩
Described by some as the Nobel prize of Mathematics, the Fields Medal is awarded every four years to up to four mathematicians under the age of forty. ↩
While Perelman was offered a Fields Medal, he notoriously did not accept it as he did not see the relevance, and is quoted as saying “I’m not interested in money or fame”. He also declined the Millennium Prize. (source) ↩
The 2019 IMO grand challenge site is still public here. ↩
See , or OpenAI’s blog. ↩
See the AlphaGeometry and AlphaProof sections of this article. ↩
See , or Meta’s blog. ↩
Another way to think about this is that any integer n, when divided by 3, must leave remainder 0, 1, or 2. ↩
Take, for example, Alfred North Whitehead and Bertrand Russell’s Principia Mathematica books, published in the second decade of the 20th century. For a popular introduction, consider reading Douglas Hofstadter’s Gödel, Escher, Bach or the graphic novel Logicomix: An Epic Search for Truth. ↩
For a history of interactive theorem proving, see . Some relevant quotes: “Almost all the earliest work on computer-assisted proof in [the 1950s and 1960s] was devoted to truly automated theorem proving”, “The increasing availability of interactive time-sharing computer operating systems in the 1960s, and later the rise of minicomputers and personal workstations was surely a valuable enabler for the development of interactive theorem proving.” ↩
This particular example was taken from , where they state that this proof would require “thirty elementary rewriting steps of the ring axioms”. In the Lean language, this automation can be achieved using the ring tactic. ↩
Other popular modern proof assistants include Isabelle, Coq, and HOL Light. This article focus on Lean given its popularity in recent machine-assisted proofs. ↩
A lemma is a proven proposition, just like a theorem. Proving a theorem can involve proving several minor “helper” lemmas along the way. The distinction between a theorem and a lemma is somewhat arbitrary, and mostly based on subjective importance. The Lean proof of nat.dvd_iff_mod_eq_zero can be found in Mathlib. ↩
This description of tactics generating proof candidates is taken from the Lean perfectoid spaces site. ↩
First through recurrent neural nets (RNNs), e.g., , and later through attention-based transformers in the Generative Pre-trained Transformer (GPT) which is now so mainstream. Andrej Karpathy’s 2015 blog post The Unreasonable Effectiveness of Recurrent Neural Networks gives a good overview of earlier generative text models operating on sequences of characters. ↩
See for details. ↩
A token is a compressed form of a chunk of text. Some tokens represent a single character; some represent multiple words. In HTPS specifically, tokenisation is done through byte-pair encoding. ↩
Google DeepMind’s blog post introducing AlphaProof and AlphaGeometry 2 can be found here. The systems’ IMO 2024 solutions are hosted here. More information is available on the Lean Zulip thread discussing the results. ↩
Source: ↩
The AlphaGeometry paper is clear that it does not attempt to solve non-Euclidean plane geometry problems: “We focus on Euclidean plane geometry and exclude topics such as geometric inequalities and combinatorial geometry”, “Geometric inequality and combinatorial geometry, for example, cannot be translated [to the formal language used by AlphaGeometry], as their formulation is markedly different to classical geometry”, “the general IMO contest also includes other types of problem, such as geometric inequality or combinatorial geometry”. ↩
A recent paper by another research group shows a purely symbolic baseline combining Wu’s method (a method published in 1978) with deductive databases and algebraic reasoning 21/30 of the problems. It lists Wu’s method as solving 15/30 problems by itself, whereas Google DeepMind’s paper credits Wu’s method with solving only 10/30. The source of the discrepancy is unclear. ↩
The AlphaProof system “performs much better on algebra and number theory than combinatorics”, and AlphaGeometry can currently only do Euclidean plane geometry problems. Quote from Google DeepMind’s Alex Davies, MIT Technology Review article, July 2024. ↩
The ABEL system , developed by researchers at Meta and elsewhere, managed to solve 7 of 640 PutnamBench problems formalised in Lean. ↩
See the missing undergraduate mathematics in mathlib page for more details. ↩
More information on Harmonic’s Series A round is available on Harmonic’s website. ↩
For example, results which hold true for both the integers and the natural numbers might be easier to prove for one than for the other. ↩
Notably, , which introduced the GSM-Symbolic benchmark: “While the performance of LLMs on GSM8K has significantly improved in recent years, it remains unclear whether their mathematical reasoning capabilities have genuinely advanced, raising questions about the reliability of the reported metrics… To address these concerns, we conduct a large-scale study on several SOTA open and closed models. … findings reveal that LLMs exhibit noticeable variance when responding to different instantiations of the same question. Specifically, the performance of all models declines when only the numerical values in the question are altered in the GSM-Symbolic benchmark.” ↩
More on o1 in this OpenAI blog post. ↩
The announcement can be seen on Mathstodon, and was explored in more depth in a Quanta article. ↩
“As with my previous formalization project, I found that the most mathematically interesting portions of the project were relatively straightforward to formalize, but it was the technical “obvious” steps that took the longest, most notably in the final stretch when we struggled to establish properties of independent random variables.” — Terence Tao, Lean Zulip ↩
Source: Terence Tao, Wordpress ↩
Taken from the Mathlib statistics page in November 2024. ↩
FLT announcement blog post ↩
A magma is “a set equipped with a single binary operation that must be closed by definition”. Groups are magmas. More on Wikipedia. ↩
The full list of contributors to the Equational Theories Project repository can be seen on GitHub. ↩
Grant application for “Formalising Fermat” ↩
“A combination of automated tools, AI tools, and interactions with human Lean experts proved invaluable. GPT greatly sped up the initial learning of syntax, tools such as exact?, apply?, and Moogle helped locate key lemmas, and Copilot had an often uncanny ability to autocomplete one or more lines of code at a time.” (Terence Tao, Mathstodon) ↩

Appel, K. I., & Haken, W. (1989). Every planar map is four colorable (Vol. 98). American Mathematical Soc. https://doi.org/https://doi.org/10.1090/conm/098

Avigad, J., & Harrison, J. (2014). Formally verified mathematics. Communications of the ACM, 57(4), 66–75.

Boyer, R., & others. (1994). The QED manifesto. Automated Deduction–CADE, 12, 238–251.

Cobbe, K., Kosaraju, V., Bavarian, M., Chen, M., Jun, H., Kaiser, L., Plappert, M., Tworek, J., Hilton, J., Nakano, R., Hesse, C., & Schulman, J. (2021). Training Verifiers to Solve Math Word Problems. https://arxiv.org/abs/2110.14168

Glazer, E., Erdil, E., Besiroglu, T., Chicharro, D., Chen, E., Gunning, A., Olsson, C. F., Denain, J.-S., Ho, A., de Oliveira Santos, E., Järviniemi, O., Barnett, M., Sandler, R., Vrzala, M., Sevilla, J., Ren, Q., Pratt, E., Levine, L., Barkley, G., … Wildon, M. (2024). FrontierMath: A Benchmark for Evaluating Advanced Mathematical Reasoning in AI. https://arxiv.org/abs/2411.04872

Gloeckle, F., Limperg, J., Synnaeve, G., & Hayat, A. (2024). ABEL: Sample Efficient Online Reinforcement Learning for Neural Theorem Proving. The 4th Workshop on Mathematical Reasoning and AI at NeurIPS’24. https://openreview.net/forum?id=kk3mSjVCUO

Gonthier, G. (2008). Formal proof–the four-color theorem. Notices of the AMS, 55(11), 1382–1393.

Gonthier, G., Asperti, A., Avigad, J., Bertot, Y., Cohen, C., Garillot, F., Le Roux, S., Mahboubi, A., O’Connor, R., Ould Biha, S., & others. (2013). A machine-checked proof of the odd order theorem. International Conference on Interactive Theorem Proving, 163–179.

Gowers, T. (2022). How can it be feasible to find proofs. https://drive.google.com/file/d/1-FFa6nMVg18m1zPtoAQrFalwpx2YaGK4

Gowers, W. T., Green, B., Manners, F., & Tao, T. (2023). On a conjecture of Marton. https://arxiv.org/abs/2311.05762

Grégoire, B., & Mahboubi, A. (2005). Proving equalities in a commutative ring done right in Coq. International Conference on Theorem Proving in Higher Order Logics, 98–113.

Hales, T. (2024). The Formal Proof of the Kepler Conjecture: a critical retrospective. https://arxiv.org/abs/2402.08032

Hales, T., Adams, M., Bauer, G., Dang, T. D., Harrison, J., Le Truong, H., Kaliszyk, C., Magron, V., McLaughlin, S., Nguyen, T. T., & others. (2017). A formal proof of the Kepler conjecture. Forum of Mathematics, Pi, 5, e2.

Harrison, J., Urban, J., & Wiedijk, F. (2014). History of Interactive Theorem Proving. In J. H. Siekmann (Ed.), Computational Logic (Vol. 9, pp. 135–214). North-Holland. https://doi.org/https://doi.org/10.1016/B978-0-444-51624-4.50004-6

Harrison, J., Urban, J., & Wiedijk, F. (2016). Preface: Twenty years of the QED manifesto. Journal of Formalized Reasoning, 9(1), 1. https://jfr.unibo.it/article/view/5974/5759

Hendrycks, D., Burns, C., Kadavath, S., Arora, A., Basart, S., Tang, E., Song, D., & Steinhardt, J. (2021). Measuring Mathematical Problem Solving With the MATH Dataset. https://arxiv.org/abs/2103.03874

Lample, G., Lachaux, M.-A., Lavril, T., Martinet, X., Hayat, A., Ebner, G., Rodriguez, A., & Lacroix, T. (2022). HyperTree Proof Search for Neural Theorem Proving. https://arxiv.org/abs/2205.11491

Mirzadeh, I., Alizadeh, K., Shahrokhi, H., Tuzel, O., Bengio, S., & Farajtabar, M. (2024). GSM-Symbolic: Understanding the Limitations of Mathematical Reasoning in Large Language Models. https://arxiv.org/abs/2410.05229

Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Antonoglou, I., Wierstra, D., & Riedmiller, M. (2013). Playing Atari with Deep Reinforcement Learning. https://arxiv.org/abs/1312.5602

Ouyang, L., Wu, J., Jiang, X., Almeida, D., Wainwright, C. L., Mishkin, P., Zhang, C., Agarwal, S., Slama, K., Ray, A., Schulman, J., Hilton, J., Kelton, F., Miller, L., Simens, M., Askell, A., Welinder, P., Christiano, P., Leike, J., & Lowe, R. (2022). Training language models to follow instructions with human feedback. https://arxiv.org/abs/2203.02155

Polu, S., Han, J. M., Zheng, K., Baksys, M., Babuschkin, I., & Sutskever, I. (2022). Formal Mathematics Statement Curriculum Learning. https://arxiv.org/abs/2202.01344

Polu, S., & Sutskever, I. (2020). Generative Language Modeling for Automated Theorem Proving. https://arxiv.org/abs/2009.03393

Ringer, T. (2024). Proofs and Conversations. Notices of the AMS. https://www.ams.org/journals/notices/202409/noti3032/noti3032.html

Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L., van den Driessche, G., Schrittwieser, J., Antonoglou, I., Panneershelvam, V., Lanctot, M., Dieleman, S., Grewe, D., Nham, J., Kalchbrenner, N., Sutskever, I., Lillicrap, T., Leach, M., Kavukcuoglu, K., Graepel, T., & Hassabis, D. (2016). Mastering the game of Go with deep neural networks and tree search. Nature, 529(7587), 484–489. https://doi.org/10.1038/nature16961

Silver, D., Hubert, T., Schrittwieser, J., Antonoglou, I., Lai, M., Guez, A., Lanctot, M., Sifre, L., Kumaran, D., Graepel, T., Lillicrap, T., Simonyan, K., & Hassabis, D. (2018). A general reinforcement learning algorithm that masters chess, shogi, and Go through self-play. Science, 362(6419), 1140–1144. https://doi.org/10.1126/science.aar6404

Sinha, S., Prabhu, A., Kumaraguru, P., Bhat, S., & Bethge, M. (2024). Wu’s Method Boosts Symbolic AI to Rival Silver Medalists and AlphaGeometry to Outperform Gold Medalists at IMO Geometry. The 4th Workshop on Mathematical Reasoning and AI at NeurIPS’24. https://openreview.net/forum?id=aKRtC45gle

Sutskever, I., Martens, J., & Hinton, G. E. (2011). Generating text with recurrent neural networks. Proceedings of the 28th International Conference on Machine Learning (ICML-11), 1017–1024. https://www.cs.utoronto.ca/~ilya/pubs/2011/LANG-RNN.pdf

Thomas, R. (1998). An update on the four-color theorem. Notices of the AMS, 45(7), 848–859. https://www.ams.org/notices/199807/thomas.pdf

Trinh, T. H., Wu, Y., Le, Q. V., He, H., & Luong, T. (2024). Solving olympiad geometry without human demonstrations. Nature, 625(7995), 476–482. https://doi.org/10.1038/s41586-023-06747-5

Tsoukalas, G., Lee, J., Jennings, J., Xin, J., Ding, M., Jennings, M., Thakur, A., & Chaudhuri, S. (2024). PutnamBench: Evaluating Neural Theorem-Provers on the Putnam Mathematical Competition. https://arxiv.org/abs/2407.11214

Wiedijk, F. (2007). The QED manifesto revisited. Studies in Logic, Grammar and Rhetoric, 10(23), 121–133. https://www.cs.ru.nl/~freek/pubs/qed2.pdf